The point of birds

@jyrimatti

There is none. They are mostly point-free!

Point?

.

or
as in point-free programming,
a point is a function argument


public static final void myFunction(String x) {...}
                                           ↑

Point-free programming?

== tacit programming

a programming paradigm in which function definitions do not identify the arguments (or "points") on which they operate. Instead the definitions merely compose other functions, among which are combinators that manipulate the arguments.

https://en.wikipedia.org/wiki/Tacit_programming

Example 1

unix pipes


echo "hello old" | tr "h" "H" | sed s/old/world/

which in Java could be:


Function<String,String> f1 = str -> str.replace('h', 'H');
Function<String,String> f2 = str -> str.replace("old", "world");
f1.andThen(f2).apply("hello old");

Example 2

Haskell


keepEven list             = filter (\x -> x `mod` 2 == 0) list
					

keepEvenPointFree         = filter (\x -> x `mod` 2 == 0)
					

keepEvenEvenMorePointFree = filter ((== 0) . (`mod` 2))

If you know Haskell and partial application,
the last one is perfectly readable.

Eta-conversion

== eta-reduction and eta-abstraction

Point-free style can be obtained via eta-reduction:
\x -> abs x ==> abs

The opposite of eta-abstraction:
abs ==> \x -> abs x

Conversion to (at least some) point-free form can be automated: http://pointfree.io

Example 3


keepHalf list = take (length list `div` 2) list
					

> nix-shell -p haskellPackages.pointfree --run \
  "pointfree -v '\list -> take (length list \`div\` 2) list'"
						

keepHalfPointFree = ap (take . flip (div . length) 2) id

🤔 Wait a second, that doesn’t look simple or easy!

 Point-free style can (clearly) lead to Obfuscation when used unwisely. ... Perhaps these are why pointfree style is sometimes (often?) referred to as pointless style.

https://wiki.haskell.org/Pointfree

Motivation

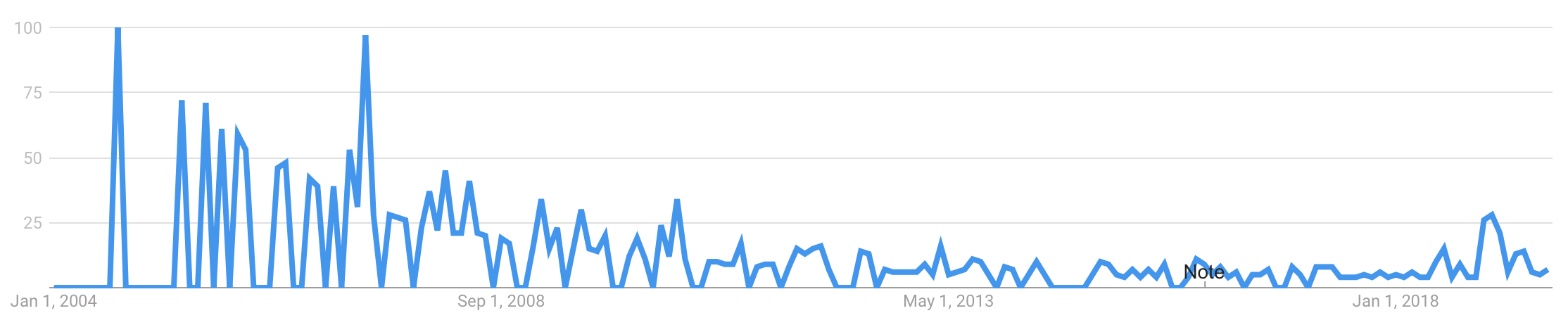
https://trends.google.com/trends/explore?date=all&q=point-free

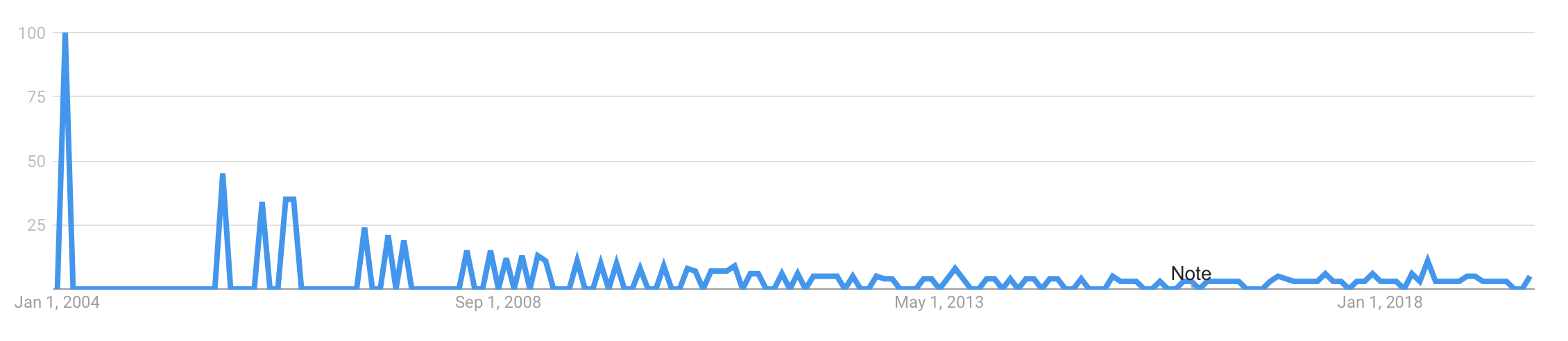
https://trends.google.com/trends/explore?date=all&q=tacit%20programming

Uh, didn't look too good...

https://trends.google.com/trends/explore?date=all&q=combinator

Let’s use this one!

Combinator?

A function or definition with no free variables == A pure lambda-expression that refers only to its arguments

https://wiki.haskell.org/Combinator

A combinator is a higher-order function that uses only function application and earlier defined combinators to define a result from its arguments.

https://en.wikipedia.org/wiki/Combinatory_logic


\a -> a
\a -> \b -> a
\f -> \a -> \b -> f b a

Lambda expression?

It is perhaps surprising that lambda-calculus can represent any conceivable computation using only the simple notions of function abstraction and application based on simple textual substitution of terms for variables. But even more remarkable is that abstraction is not even required. Combinatory logic is a model of computation equivalent to lambda calculus, but without abstraction.

https://en.wikipedia.org/wiki/Combinatory_logic

Combinatory logic?

no abstraction == no creation of lambdas
== no function arguments

But the example combinators on the previous slide were lambdas themselves!?!

Yes, but we assume that there exists a primitive set of combinators, from which more can be built without lambda abstraction.

How big is this primitive set?

Sidetrack: K?

Lambda calculus is sometimes also called λK-calculus, meaning that in combinator logic there’s a K combinator involved.

K x y = x

K is cancellative, it doesn’t use one of it’s arguments.

In λI-calculus, there’s no K
(that is, all arguments must be used)

Naming things is hard?

Single-letter-names are a bit mathy.

Raymond m. Smullyan: To Mock a Mockingbird

I
Idiot x = x
K
Kestrel x y = x
I*
IdiotOnceRemoved x y = x y
T
Thrust x y = y x
C
Cardinal x y z = x z y
B
Bluebird x y z = x (y z)
Q
Queer x y z = y (x z)
B
Blackbird x y z w = x (y z w)
...

Kestrel1.jpg
By Ryser915 at English Wikipedia, CC BY-SA 3.0, Link

Medium sized songbird stands upright with greyish upperbody, blackened wings, white underparts streaked with black, a white face with a prominent black crescent behind the eye and black line running from the eye down, and grey bill with yellow below
By Yathin S Krishnappa - Own work, CC BY-SA 3.0, Link

Northern Cardinal Broadside.jpg
By Dakota L. - Own work, CC BY-SA 3.0, Link

Eastern Bluebird.jpg
By Dehaan - Own work, CC BY-SA 3.0, Link

Turdus merula -Gran Canaria, Canary Islands, Spain-8 (2).jpg
By Juan Emilio from Las Palmas de Gran Canaria, España - Mirlo. (Turdus merula cabrerae.)(♂)Uploaded by Snowmanradio, CC BY-SA 2.0, Link

A combinator for keepHalf?


keepHalf list     = take (length list `div` 2) list
keepHalfPointFree = ap (take . flip (div . length) 2) id

phoenix == pass a single value through two different functions,
and pass the results to a two-parameter function


phoenix x y z w = x (y w) (z w)
keepHalfCombi = phoenix take ((`div` 2) . length) id

starling == pass a single value straight and also through a function, to a two-parameter function


starling = x y z = x z (y z)
keepHalfCombi2 = starling (flip take) ((`div` 2) . length)

cardinal' == pass first argument straight, and second argument through a function,
to a two-parameter function

warbler == elementary duplicator


cardinal' x y z w = x (y w) z
warbler x y = x y y
keepHalfCombi3 = warbler $ cardinal' take ((`div` 2) . length)

There might be a day, when these are taught in the universities and we all know all these combinators by heart!

...meanwhile, is there something easier?

Starling == Applicative's (<*>) on functions

Like ordinary application of take with two arguments:


keepHalf list = take (length list `div` 2) list

but instead we use kind of lifted function application,
syntactically with operators <$> and <*>:


keepHalfApplicative = take <$> ((`div` 2) . length) <*> id

This is actually readable!

By abstracting over function application in our language, we might not even need the operators...

Visualisation

Can be visualised as data flow


nix-shell --pure -p graphviz --run 'echo "digraph g{\
	rankdir=\"LR\";\
	\"input-list\" -> \"((\`div\` 2) . length)\";\
	\"((\`div\` 2) . length)\" -> \"take :: Int -> [a] -> [a]\";\
	\"input-list\" -> \"take :: Int -> [a] -> [a]\";\
	\"take :: Int -> [a] -> [a]\" -> \"result-list\"\
}" | dot -Tsvg > graph.svg'

Imagine your editor/IDE to automatically visualize all Applicative-function usages with this kind of (even interactive) graphics!

a missing bird?

Each previous example had something awkward


missingBird :: (b -> a -> c) -> (a -> b) -> a -> c
missingBird x y z = x (y z) z

keepHalfCombi4 = missingBird take ((`div` 2) . length)

I couldn't find references to this kind of combinator...?

Example 4


-- from Haskell base:
sortBy :: (a -> a -> Ordering) -> [a] -> [a]

someListOfTuples = [(1,'a'), (2,'b')]

sortedByNumberVerbose = sortBy (\t1 t2 -> compare (fst t1) (fst t2)) someListOfTuples

Do we happen to have a combinator for:
Pass both parameters through same function,
and pass the results to a two-parameter function?


psi x y z w = x (y z) (y w)
sortedByNumberCombinator = sortBy (psi compare fst) someListOfTuples

This need was recognised ages ago

There’s already a psi bird with a different name in Haskell base: on 


-- http://hackage.haskell.org/package/base/docs/Data-Function.html#v:on
sortedByNumberOn = sortBy (compare `on` fst) someListOfTuples
					

nix-shell --pure -p graphviz --run 'echo "digraph g{\
	rankdir=LR;\
	\"compare\" -> \"on :: (b -> b -> Ordering) -> (a -> b) -> a -> a -> Ordering\";\
	\"fst\" -> \"on :: (b -> b -> Ordering) -> (a -> b) -> a -> a -> Ordering\";\
	\"on :: (b -> b -> Ordering) -> (a -> b) -> a -> a -> Ordering\" -> \"sortBy :: (a -> a -> Ordering) -> [a] -> [a]\";\
	\"input-list\" -> \"sortBy :: (a -> a -> Ordering) -> [a] -> [a]\";\
	\"sortBy :: (a -> a -> Ordering) -> [a] -> [a]\" -> \"result-list\"\
}" | dot -Tsvg > graph2.svg'

Example 5

"Point-Free or Die: Tacit Programming in Haskell and Beyond" by Amar Shah

aggregation == first map over the function f,
then sum the resulting numbers


aggregate f list = sum (map f list)

in point-free style?

 

aggregate f = sum . map f
aggregate   = (sum .) . map

Would we happen to have a combinator for:
pass two parameters to a two-parameter function, and then pass the result to a one-parameter function? 


blackbird x y z w = x (y z w)

blackbird == composition of composition and composition

(.) . (.)

Yeah right, but the visualisation is clear

a coincidence?

A function with the same type signature as blackbird happens to be defined in multiple Hackage packages with different name.

Could it be useful to have it defined in base with a suitable name, like that suggested by Amar Shah:


f ... g = (f .) . g

Summary

  • Point-free style == tacit programming == no function arguments
  • Point-free style can be extremely readable
  • Excessive use of point-free style is bad for readability
    - especially if one blindly takes what automatic tools provide
  • Knowledge of some basic building blocks is needed to figure out proper abstractions
    - why oh why don’t they teach these to everyone in the university?
  • Combinators are often communicated by using names of specific birds
  • Higher-level abstractions built from combinators might be more useful. For example:
    - Applicative Functor of functions is awesome
    - `on`
    - blackbird
  • Using point-free style might bring opportunities for code visualisation

Links & References

Forget that cutting edge JavaScript framework!
Learn you a fundamental tool for great good!

Thank you.

link to this presentation: https://lahteenmaki.net/dev_*19/