Curse explicit recursion!
dev* 2018
What is recursion?
Yeah, old joke...
What is recursion?
Recursion in computer science is a method of solving a problem where the solution depends on solutions to smaller instances of the same problem (as opposed to iteration). The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science. |
🤔 |
Factorial with iteration, in Java
int factorial(int n) {
int res = 1;
for (int i=1; i<=n; i++) {
res = res * i;
}
return res;
}
With mutation included, as iteration often does.

Standard response of functional languages: recursion!
factorial 0 = 1
factorial n = n * factorial (n-1)
Maybe elegant but there's a problem...
It's not tail recursive -> will blow up stack usage
Recursive list length
(define (length lst)
(cond
[(empty? lst) 0]
[else (+ 1 (length lst))]))
But there’s a bug not easily seen!
This is in Scheme, so is this a...
•_•)
( •_•)>⌐■-■
(⌐■_■)
... Recursion Scheme?
Recursion is dangerous!
Do we really need recursion?
factorial n = foldr (*) 1 [1..n]
No recursion to be seen! But what is this “fold” thing?
- Fold hides the recursion in a safe wrapping
- Fold is actually something called a catamorphism
- There are other wrappers. Ever heard of an unfold?
more Haskell factorials: https://www.willamette.edu/~fruehr/haskell/evolution.html
Can we “package” all kinds of recursion?
Could we even have a usable programming language without any kind of explicit recursive calls?
I have no idea 🙂
But why?
- separatation of concerns
- separate actual algorithm from the recursive part
- e.g. for length the "business logic” is:
1 + length_of_rest_of_the_list - cleaner!
- generally usable with different structures (trees?)
Recursion Schemes
Brief and incomplete history
- 1987: Name catamorphism appears in a paper by Lambert Meertens
- 1990: The category theoretic machinery behind these was resolved by Grant Malcolm
- 1991: Meijer, Fokkinga and Paterson publish their famous paper
Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire - 1999: Histomorphism and Futumorphism are introduced by Uustalu & Venu
- 2011: Edward Kmett releases the first version of recursion-schemes library
- 2012: Hinze et al. publish a paper and another describing sorting algorithms in recursion schemes
- 2014: First part of the excellent blog series is published
- 2018: Lot's of blog and conference activity!
Is this still pop?
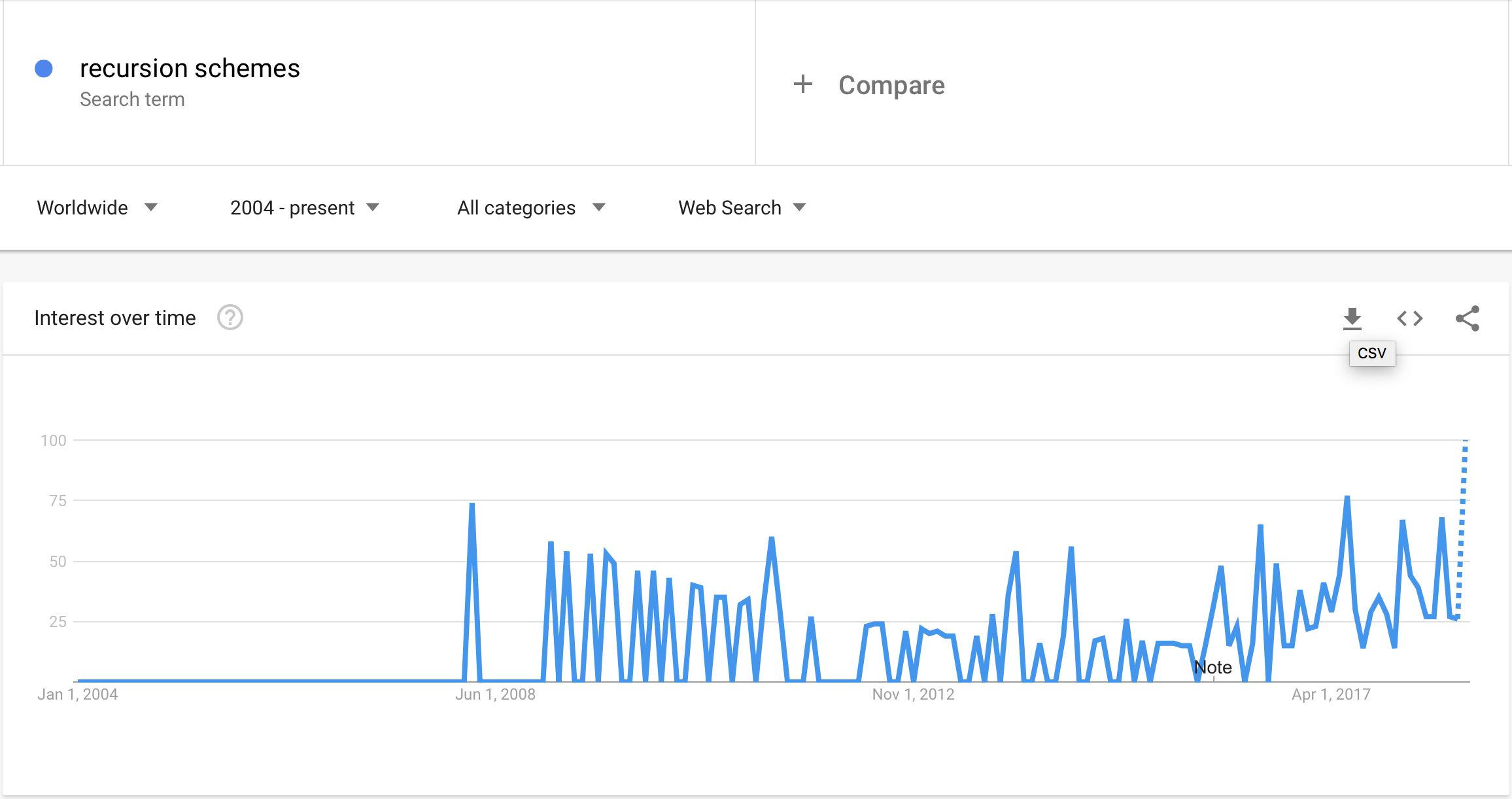
Is this still pop?
Implementing some use cases
For these examples we need something called
a fix point
newtype Fix f = Fix (f (Fix f))
-- Wrap value inside a Fix point
fix :: f (Fix f) -> Fix f
fix = Fix
-- Unwrap value from a Fix point
unfix :: Fix f -> f (Fix f)
unfix (Fix f) = f
Learning about it is left as an exercise for the reader 😉
Example 1: sum of a list of numbers (catamorphism)
-- Familiar cons-list. No need to make this, but as an example...
data MyListF elem rest = NilF | ConsF elem rest deriving Functor
type List t = Fix (MyListF t)
nil = Fix NilF -- make an empty list
cons x xs = Fix (ConsF x xs) -- cons a value in front of a list
-- our "algorithm" to sum list elements would be just:
sumAlg = \case
NilF -> 0 -- sum of an empty list is 0
ConsF x xs -> x + xs -- add the current value to others
-- execute our algorithm by giving it to some library function
exampleSum = doStuff sumAlg
-- > exampleSum (cons 4 $ cons 12 $ cons 7 nil) -- [4, 12, 7]
-- 23Example 1: sum of a list of numbers (catamorphism)
-- This general library function still needs explicit recursion
doStuff alg = unfix >>> -- unwrap from the Fix point
fmap (doStuff alg) -- apply algorithm recursively
>>> alg -- apply to the final value
-- "alg" was not an abreviation of "algorithm", but of "Algebra"
type Algebra f a = f a -> a
-- Complete implementation for 'sum' would thus be the
-- following (using recursion-schemes library), which neatly
-- contains only the algorithmic part without any recursion
sum :: [Int] -> Int
sum = cata $ \case
Nil -> 0
Cons x xs -> x + xsSum is just a regular fold, so the famous fold is just one of the recursion schemes, namely catamorphism!
Reminder: Many things come in pairs

Example 2: natural numbers (anamorphism)
-- Stream of natural numbers
data StreamF r = StreamF Natural r deriving Functor
type NatStream = Fix StreamF
-- our "algorithm" to create numbers would be
naturalsCoalg n = StreamF n (n + 1) -- for each n, next is n+1
-- same as before, seed value zero
exampleNats = doStuff naturalsCoalg 0
-- unfortunately in this example our numbers are our NatStream,
-- but we can convert it to a Haskell list with a catamorphism
exampleNaturals = cata (\case StreamF x xs -> x:xs) exampleNats
-- > take 4 exampleNaturals
-- [0,1,2,3]Example 2: natural numbers (anamorphism)
-- Dual of catamorphism:
-- 1) arrows are reversed
-- 2) wrap instead of unwrap
doStuff coalg = Fix <<< fmap (doStuff coalg) <<< coalg
-- "coalg" is called a "Coalgebra"
type Coalgebra f a = a -> f a
-- Complete implementation using recursion-schemes library:
naturals :: [Natural]
naturals = ana (\n -> Cons n (n + 1)) 0
So, generating an infinite stream is just one of the recursion schemes, namely anamorphism!
Sidetrack: fan out operator
in Data.Tuple.Extra
or Control.Arrow
or Control.Category.Cartesian
-- for functions:
(&&&) :: (a -> b) -> (a -> c) -> a -> (b, c)
-- for any category:
(&&&) :: a b c -> a b c' -> a b (c, c')
"split a value to two different paths”
Example 3: factorial (paramorphism)
-- Natural numbers as Peano
data NatF r = ZeroF | SuccF r deriving Functor
type Nat = Fix NatF
zero = Fix ZeroF
succ = Fix . SuccF
factorialAlg = \case
ZeroF -> 1
SuccF (cur, r) -> (toNat cur + 1) * r
-- unfortunately our example numbers are Peano, but we
-- can use catamorphism to transform to regular numbers
where toNat = cata $ \case
ZeroF -> 0
SuccF n -> n + 1
exampleFactorial = doStuff factorialAlg
-- > exampleFactorial (succ (succ (succ zero))) -- 3
-- 6Example 3: factorial (paramorphism)
doStuff alg = unfix >>> fmap (id &&& doStuff alg) >>> alg
-- here "alg" is called an "RAlgebra"
type RAlgebra f a = f (Fix f, a) -> a
-- Complete implementation using recursion-schemes library:
factorial :: Natural -> Natural
factorial = para $ \case
Nothing -> 1
Just (n, r) -> (n+1) * r
Thus, catamorphism with access to the current input value is called a paramorphism!
Sidetrack: fan in operator
dual for fan out
in Control.Arrow
or Control.Category.Cartesian
(|||) :: a b d -> a c d -> a (Either b c) d
“split a value to one of two different paths”
Example 4: numeric range (apomorphism)
rangeCoalg to = \case
n | n == to -> ConsF n (Left nil)
n -> ConsF n (Right (n + 1))
exampleRange_ from to = doStuff (rangeCoalg to) from
-- have to convert our List type to the Haskell list again...
exampleRange from to = cata (\case
NilF -> []
ConsF x xs -> x:xs
) (exampleRange_ from to)
-- > exampleRange 0 4
-- [0,1,2,3,4]Example 4: numeric range (apomorphism)
doStuff coalg = Fix <<< fmap (id ||| doStuff coalg) <<< coalg
-- here "coalg" is called an "RCoalgebra":
type RCoalgebra f a = a -> f (Either (Fix f) a)
-- Complete implementation using recursion-schemes library:
range :: Int -> Int -> [Int]
range from to = flip apo from $ \case
n | n == to -> Cons n (Left [])
n -> Cons n (Right (n + 1))That is: anamorphism terminating at some chosen point, is called an apomorphism!
Sidetrack: Freedom!
Free Monad:
data Free f a = Pure a | Free (f (Free f a))
Cofree Comonad:
data Cofree f a = a :< (f (Cofree f a))
Kind of minimal way to provide monadic or comonadic structure
Example 5: fibonacci (histomorphism)
Sometimes we need access to the previous values
-- using Cofree Comonad here to bring comonadic structure...
fibonacciAlg ZeroF = 0
fibonacciAlg (SuccF (_ :< ZeroF)) = 1
fibonacciAlg (SuccF (a :< SuccF (b :< _))) = a + b
exampleFibonacci = doStuff fibonacciAlg
-- > exampleFibonacci (succ (succ (succ zero))) -- 3
-- 2
Example 5: fibonacci (histomorphism)
doStuff alg = f >>> (\(x :< _) -> x)
where f = unfix >>> fmap f >>> (alg &&& id) >>> uncurry (:<)
-- here "alg" is called a "CVAlgebra"
type CVAlgebra f a = f (Cofree f a) -> a
-- Complete implementation using recursion-schemes library:
fibonacci :: Natural -> Natural
fibonacci = histo $ \case
Nothing -> 0
Just (_ :< Nothing) -> 1
Just (a :< Just (b :< _)) -> a + b
Paramorphism providing the whole history instead of the current value is called a histomorphism!
Example 6: capitalizeWords (futumorphism)
Apomorphism let us terminate once, but now we need to terminate multiple times with a value (word)
capitalizeWordsCoalg "" = NilF
capitalizeWordsCoalg str = let
ws = words str
(first,rest) = (head ws, tail ws)
capitalized = toUpper (head first) : tail first
in ConsF capitalized (Pure $ unwords rest)
exampleCapitalizeWords_ = doStuff capitalizeWordsCoalg
exampleCapitalizeWords str = unwords $ cata (\case
NilF -> []
ConsF x xs -> x:xs
) (exampleCapitalizeWords_ str)
-- > exampleCapitalizeWords "foo bar"
-- "Foo Bar"Example 6: capitalizeWords (futumorphism)
doStuff coalg = Fix <<< fmap worker <<< coalg
where worker (Pure a) = doStuff coalg a
worker (Free a) = Fix (fmap worker a)
-- here "coalg" is called a "CVCoalgebra":
type CVCoalgebra f a = a -> f (Free f a)
-- Complete implementation using recursion-schemes library:
capitalizeWords :: String -> String
capitalizeWords = unwords . futu (\case
"" -> Nil
str -> let ws = words str
(first,rest) = (head ws, tail ws)
capitalized = toUpper (head first) : tail first
in Cons capitalized (Pure $ unwords rest))Whereas histomorphism extended paramorphism to the whole history, futumorphism extends apomorphism to the whole future!
Example 7: takeWhile (prepromorphism)
-- filtering of a List-functor with a predicate function
filter _ Nil = Nil
filter pred x@(Cons h _)
| pred h = x
| otherwise = Nil
takeWhile :: (a -> Bool) -> [a] -> [a]
takeWhile pred = prepro (filter pred) $ \case
Nil -> []
(Cons x xs) -> x:xs
Prepromorphism is like a catamorphism but executes a natural transformation before the actual stuff
Example 8: first 10 natural numbers (postpromorphism)
With Apomorphism we could terminate the recursion, but it would be nicer if we could work on infinite streams and cap them with an external function.
-- use whatever generator function
generate f n = Cons n (f n)
-- now both filtering and stream generation are nicely separated from recursion
range :: (Num a, Ord a) => a -> a -> [a]
range from to = postpro (filter (<= to)) (generate (+1)) from
Postpromorphism is like an anamorphism but executes a natural transformation after the actual stuff
hylomorphism
Many times a problem involves multiple recursions.
For example: Merge sort
- unfold with anamorphism
- fold with catamorphism
using ana + cata is called a hylomorphism
hylomorphism
hylo :: Functor f => Algebra f b -> Coalgebra f a -> a -> b
hylo alg coalg = ana coalg >>> cata alg
Can be implemented without actually invoking cata or ana.
Also it seems that the compiler can optimize away all our imaginary structure used to define Algebra and Coalgebra! *
* http://fho.f12n.de/posts/2014-05-07-dont-fear-the-cat.html
chronomorphism
One can also combine Futumorphism + Histomorphism:
chrono :: Functor f => CVAlgebra f b -> CVCoalgebra f a -> a -> b
chrono cvalg cvcoalg = futu cvcoalg >>> histo cvalg
Elgot algebras
Sometimes we need to short circuit our hylomorphism during construction
elgot :: Functor f => Algebra f b -> (a -> Either b (f a)) -> a -> b
or during destruction
coelgot :: Functor f => ((a, f b) -> b) -> Coalgebra f a -> a -> b
Sorting
Sorting algorithms tend to be different combinations of specific recursion patterns.
Many (if not all?) sorting algorithms can be defined elegantly with suitable recursion schemes.
| merge-sort | hylomorfismi |
| quick-sort | hylomorfismi |
| insertion-sort | apomorfismi |
| selection-sort | paramorphism |
data vs codata
| data | finite |
| codata | infinite |
Different algebras deal with data. They provide recursion.
Different coalgebras deal with codata. They provide corecursion.
Some functions are total for data but not for codata (e.g. length).
Some functions are total for codata but not for data (e.g. head).
data vs codata
In a total language (not Haskell!) the difference is important, since all functions must always terminate and never fail.
If our language separated data and codata,
could we have safe recursion for data and safe corecursion for codata?!?
Summary
| catamorphism | “romauttaminen” | type Algebra f a = f a -> a |
| anamorphism | “hajauttaminen” | type Coalgebra f a = a -> f a |
| paramorphism | “liittäminen” | type RAlgebra f a = f (Fix f, a) -> a |
| apomorphism | “erottaminen” | type RCoalgebra f a = a -> f (Either (Fix f) a) |
| histomorphism | “historia” | type CVAlgebra f a = f (Cofree f a) -> a |
| futumorphism | “tulevaisuus” | type CVCoalgebra f a = a -> f (Free f a) |
| prepromorphism | “esikäsittely” | |
| postpromorphism | “jälkikäsittely” | |
| hylomorphism | “hajauttaminen + romauttaminen” | |
| chronomorphism | “tulevaisuus + historia” | |
zygomorphism, dynamorphism, codynamorphism, elgot algebra, elgot coalgebra, metamorphism, synchromorphism, exomorphism, mutumorphism, ...
Summary
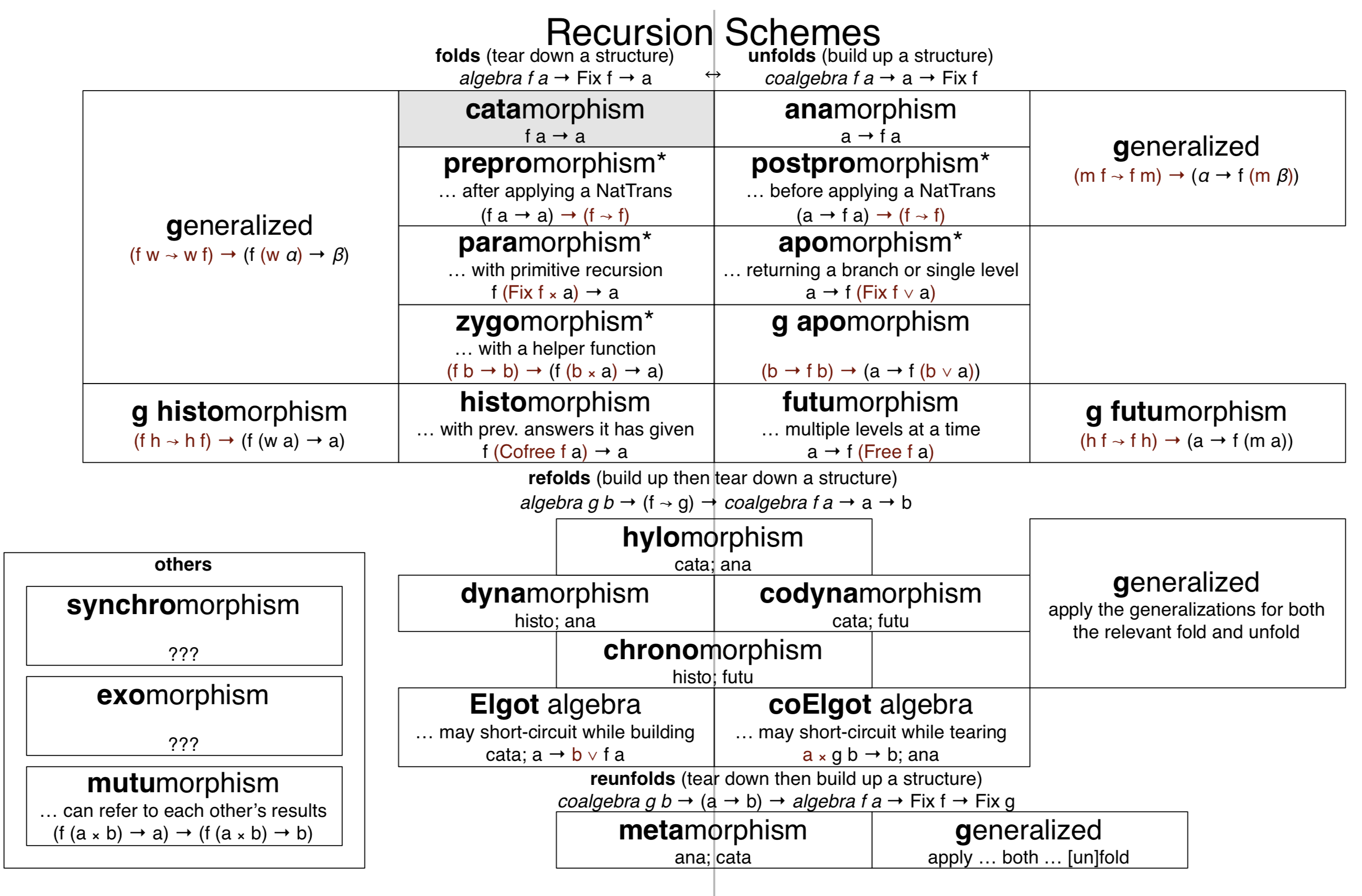
https://github.com/sellout/recursion-scheme-talk/blob/master/cheat%20sheet.pdf
Reading material for passionate souls
- Cheat sheet
- https://github.com/sellout/recursion-scheme-talk/blob/master/cheat%20sheet.pdf
- First mention of catamorphism
- https://www.researchgate.net/publication/238688759_First_steps_towards_the_theory_of_rose_trees
- Data structures and program transformation
- https://www.sciencedirect.com/science/article/pii/0167642390900237
- Algebraic Data Types and Program Transformation
- http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.221.4281&rep=rep1&type=pdf
- Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire
- http://maartenfokkinga.github.io/utwente/mmf91m.pdf
- Primitive (Co)Recursion and Course-of-Value (Co)Iteration, Categorically (Uustalu, Vene)
- https://informatica.vu.lt/journal/INFORMATICA/article/256/file/pdf
- Hinze et al. describing sorting algorithms in recursion schemes
- paper and another
- Great blog series, which I can understand (7 parts)
- https://blog.sumtypeofway.com/an-introduction-to-recursion-schemes/
- More readable blog posts
- practical-recursion-schemes, promorphisms-pre-post and time-for-chronomorphisms
- Table of recursion schemes
- http://comonad.com/reader/2009/recursion-schemes/
- Elgot algebras
- https://arxiv.org/pdf/cs/0609040.pdf
- Edward Kmett’s Haskell library
- http://hackage.haskell.org/package/recursion-schemes
- About data vs codata
- https://www.tac-tics.net/blog/data-vs-codata
http://blog.sigfpe.com/2007/07/data-and-codata.html - A curation of useful resources for learning about and using recursion schemes
- https://github.com/passy/awesome-recursion-schemes
- About catamorphisms
- https://www.schoolofhaskell.com/user/edwardk/recursion-schemes/catamorphisms
- edit 2025: Recursion Schemes from Comonads (Uustalu et al)
- https://www.researchgate.net/publication/220673192_Recursion_Schemes_from_Comonads
- edit 2025: An approachable intro to different recursion schemes
- Fantastic Morphisms and Where to Find Them - A Guide to Recursion Schemes
Remember to learn
a category theoretical thing
every year ;)
Thank you!